CEDMAV Publications
2018


K Knudson, B Wang.
“Discrete Stratified Morse Theory: A User's Guide,” In CoRR, 2018.
Inspired by the works of Forman on discrete Morse theory, which is a combinatorial adaptation to cell complexes of classical Morse theory on manifolds, we introduce a discrete analogue of the stratified Morse theory of Goresky and MacPherson (1988). We describe the basics of this theory and prove fundamental theorems relating the topology of a general simplicial complex with the critical simplices of a discrete stratified Morse function on the complex. We also provide an algorithm that constructs a discrete stratified Morse function out of an arbitrary function defined on a finite simplicial complex; this is different from simply constructing a discrete Morse function on such a complex. We borrow Forman's idea of a "user's guide," where we give simple examples to convey the utility of our theory.


S. Kumar, A. Humphrey, W. Usher, S. Petruzza, B. Peterson, J. A. Schmidt, D. Harris, B. Isaac, J. Thornock, T. Harman, V. Pascucci,, M. Berzins.
“Scalable Data Management of the Uintah Simulation Framework for Next-Generation Engineering Problems with Radiation,” In Supercomputing Frontiers, Springer International Publishing, pp. 219--240. 2018.
ISBN: 978-3-319-69953-0
DOI: 10.1007/978-3-319-69953-0_13
The need to scale next-generation industrial engineering problems to the largest computational platforms presents unique challenges. This paper focuses on data management related problems faced by the Uintah simulation framework at a production scale of 260K processes. Uintah provides a highly scalable asynchronous many-task runtime system, which in this work is used for the modeling of a 1000 megawatt electric (MWe) ultra-supercritical (USC) coal boiler. At 260K processes, we faced both parallel I/O and visualization related challenges, e.g., the default file-per-process I/O approach of Uintah did not scale on Mira. In this paper we present a simple to implement, restructuring based parallel I/O technique. We impose a restructuring step that alters the distribution of data among processes. The goal is to distribute the dataset such that each process holds a larger chunk of data, which is then written to a file independently. This approach finds a middle ground between two of the most common parallel I/O schemes--file per process I/O and shared file I/O--in terms of both the total number of generated files, and the extent of communication involved during the data aggregation phase. To address scalability issues when visualizing the simulation data, we developed a lightweight renderer using OSPRay, which allows scientists to visualize the data interactively at high quality and make production movies. Finally, this work presents a highly efficient and scalable radiation model based on the sweeping method, which significantly outperforms previous approaches in Uintah, like discrete ordinates. The integrated approach allowed the USC boiler problem to run on 260K CPU cores on Mira.


S. Liu, P.T. Bremer, J.J. Thiagarajan, V. Srikumar, B. Wang, Y. Livnat, V. Pascucci.
“Visual Exploration of Semantic Relationships in Neural Word Embeddings,” In IEEE Transactions on Visualization and Computer Graphics, Vol. 24, No. 1, IEEE, pp. 553--562. Jan, 2018.
DOI: 10.1109/tvcg.2017.2745141
Constructing distributed representations for words through neural language models and using the resulting vector spaces for analysis has become a crucial component of natural language processing (NLP). However, despite their widespread application, little is known about the structure and properties of these spaces. To gain insights into the relationship between words, the NLP community has begun to adapt high-dimensional visualization techniques. In particular, researchers commonly use t-distributed stochastic neighbor embeddings (t-SNE) and principal component analysis (PCA) to create two-dimensional embeddings for assessing the overall structure and exploring linear relationships (e.g., word analogies), respectively. Unfortunately, these techniques often produce mediocre or even misleading results and cannot address domain-specific visualization challenges that are crucial for understanding semantic relationships in word embeddings. Here, we introduce new embedding techniques for visualizing semantic and syntactic analogies, and the corresponding tests to determine whether the resulting views capture salient structures. Additionally, we introduce two novel views for a comprehensive study of analogy relationships. Finally, we augment t-SNE embeddings to convey uncertainty information in order to allow a reliable interpretation. Combined, the different views address a number of domain-specific tasks difficult to solve with existing tools.


S. Petruzza, A. Gyulassy, V. Pascucci,, P. T. Bremer.
“A Task-Based Abstraction Layer for User Productivity and Performance Portability in Post-Moore’s Era Supercomputing,” In 3RD INTERNATIONAL WORKSHOP ON POST-MOORE’S ERA SUPERCOMPUTING (PMES), 2018.
The proliferation of heterogeneous computing architectures in current and future supercomputing systems dramatically increases the complexity of software development and exacerbates the divergence of software stacks. Currently, task-based runtimes attempt to alleviate these impediments, however their effective use requires expertise and deep integration that does not facilitate reuse and portability. We propose to introduce a task-based abstraction layer that separates the definition of the algorithm from the runtime-specific implementation, while maintaining performance portability.


S. Petruzza, A. Gyulassy, V. Pascucci,, P. T. Bremer.
“A Task-Based Abstraction Layer for User Productivity and Performance Portability in Post-Moore’s Era Supercomputing,” In 3RD INTERNATIONAL WORKSHOP ON POST-MOORE’S ERA SUPERCOMPUTING (PMES), 2018.
The proliferation of heterogeneous computing architectures in current and future supercomputing systems dramatically increases the complexity of software development and exacerbates the divergence of software stacks. Currently, task-based runtimes attempt to alleviate these impediments, however their effective use requires expertise and deep integration that does not facilitate reuse and portability. We propose to introduce a task-based abstraction layer that separates the definition of the algorithm from the runtime-specific implementation, while maintaining performance portability.


B. Summa, N. Faraj, C. Licorish, V. Pascucci.
“Flexible Live‐Wire: Image Segmentation with Floating Anchors,” In Computer Graphics Forum, Vol. 37, No. 2, Wiley, pp. 321-328. May, 2018.
DOI: 10.1111/cgf.13364
We introduce Flexible Live‐Wire, a generalization of the Live‐Wire interactive segmentation technique with floating anchors. In our approach, the user input for Live‐Wire is no longer limited to the setting of pixel‐level anchor nodes, but can use more general anchor sets. These sets can be of any dimension, size, or connectedness. The generality of the approach allows the design of a number of user interactions while providing the same functionality as the traditional Live‐Wire. In particular, we experiment with this new flexibility by designing four novel Live‐Wire interactions based on specific primitives: paint, pinch, probable, and pick anchors. These interactions are only a subset of the possibilities enabled by our generalization. Moreover, we discuss the computational aspects of this approach and provide practical solutions to alleviate any additional overhead. Finally, we illustrate our approach and new interactions through several example segmentations.


W Usher, P Klacansky, F Federer, PT Bremer, A Knoll, J. Yarch, A. Angelucci, V. Pascucci .
“A virtual reality visualization tool for neuron tracing,” In IEEE Transactions on Visualization and Computer Graphics, Vol. 24, No. 1, IEEE, pp. 994--1003. Jan, 2018.
DOI: 10.1109/tvcg.2017.2744079
racing neurons in large-scale microscopy data is crucial to establishing a wiring diagram of the brain, which is needed to understand how neural circuits in the brain process information and generate behavior. Automatic techniques often fail for large and complex datasets, and connectomics researchers may spend weeks or months manually tracing neurons using 2D image stacks. We present a design study of a new virtual reality (VR) system, developed in collaboration with trained neuroanatomists, to trace neurons in microscope scans of the visual cortex of primates. We hypothesize that using consumer-grade VR technology to interact with neurons directly in 3D will help neuroscientists better resolve complex cases and enable them to trace neurons faster and with less physical and mental strain. We discuss both the design process and technical challenges in developing an interactive system to navigate and manipulate terabyte-sized image volumes in VR. Using a number of different datasets, we demonstrate that, compared to widely used commercial software, consumer-grade VR presents a promising alternative for scientists.


W. Usher, S. Rizzi, I. Wald, J. Amstutz, J. Insley, V. Vishwanath, N. Ferrier, M. E. Papka,, V. Pascucci.
“libIS: A Lightweight Library for Flexible In Transit Visualization,” In Proceedings of the Workshop on In Situ Infrastructures for Enabling Extreme-Scale Analysis and Visualization, ACM Press, 2018.
DOI: 10.1145/3281464.3281466
As simulations grow in scale, the need for in situ analysis methods to handle the large data produced grows correspondingly. One desirable approach to in situ visualization is in transit visualization. By decoupling the simulation and visualization code, in transit approaches alleviate common difficulties with regard to the scalability of the analysis, ease of integration, usability, and impact on the simulation. We present libIS, a lightweight, flexible library which lowers the bar for using in transit visualization. Our library works on the concept of abstract regions of space containing data, which are transferred from the simulation to the visualization clients upon request, using a client-server model. We also provide a SENSEI analysis adaptor, which allows for transparent deployment of in transit visualization. We demonstrate the flexibility of our approach on batch analysis and interactive visualization use cases on different HPC resources.
2017


S. Kumar, D. Hoang, S. Petruzza, J. Edwards, V. Pascucci.
“Reducing Network Congestion and Synchronization Overhead During Aggregation of Hierarchical Data,” In 2017 IEEE 24th International Conference on High Performance Computing (HiPC), pp. 223-232. Dec, 2017.
DOI: 10.1109/HiPC.2017.00034
Hierarchical data representations have been shown to be effective tools for coping with large-scale scientific data. Writing hierarchical data on supercomputers, however, is challenging as it often involves all-to-one communication during aggregation of low-resolution data which tends to span the entire network domain, resulting in several bottlenecks. We introduce the concept of indexing templates, which succinctly describe data organization and can be used to alter movement of data in beneficial ways. We present two techniques, domain partitioning and localized aggregation, that leverage indexing templates to alleviate congestion and synchronization overheads during data aggregation. We report experimental results that show significant I/O speedup using our proposed schemes on two of today's fastest supercomputers, Mira and Shaheen II, using the Uintah and S3D simulation frameworks.


S. Kumar, D. Hoang, S. Petruzza, J. Edwards, V. Pascucci.
“Reducing network congestion and synchronization overhead during aggregation of hierarchical data,” In 2017 IEEE 24th International Conference on High Performance Computing (HiPC), IEEE, Dec, 2017.
DOI: 10.1109/hipc.2017.00034
Hierarchical data representations have been shown to be effective tools for coping with large-scale scientific data. Writing hierarchical data on supercomputers, however, is challenging as it often involves all-to-one communication during aggregation of low-resolution data which tends to span the entire network domain, resulting in several bottlenecks. We introduce the concept of indexing templates, which succinctly describe data organization and can be used to alter movement of data in beneficial ways. We present two techniques, domain partitioning and localized aggregation, that leverage indexing templates to alleviate congestion and synchronization overheads during data aggregation. We report experimental results that show significant I/O speedup using our proposed schemes on two of today's fastest supercomputers, Mira and Shaheen II, using the Uintah and S3D simulation frameworks.


S. Petruzza, A. Venkat, A. Gyulassy, G. Scorzelli, F. Federer, A. Angelucci, V. Pascucci, P. T. Bremer.
“ISAVS: Interactive Scalable Analysis and Visualization System,” In ACM SIGGRAPH Asia 2017 Symposium on Visualization, ACM Press, 2017.
DOI: 10.1145/3139295.3139299
Modern science is inundated with ever increasing data sizes as computational capabilities and image acquisition techniques continue to improve. For example, simulations are tackling ever larger domains with higher fidelity, and high-throughput microscopy techniques generate larger data that are fundamental to gather biologically and medically relevant insights. As the image sizes exceed memory, and even sometimes local disk space, each step in a scientific workflow is impacted. Current software solutions enable data exploration with limited interactivity for visualization and analytic tasks. Furthermore analysis on HPC systems often require complex hand-written parallel implementations of algorithms that suffer from poor portability and maintainability. We present a software infrastructure that simplifies end-to-end visualization and analysis of massive data. First, a hierarchical streaming data access layer enables interactive exploration of remote data, with fast data fetching to test analytics on subsets of the data. Second, a library simplifies the process of developing new analytics algorithms, allowing users to rapidly prototype new approaches and deploy them in an HPC setting. Third, a scalable runtime system automates mapping analysis algorithms to whatever computational hardware is available, reducing the complexity of developing scaling algorithms. We demonstrate the usability and performance of our system using a use case from neuroscience: filtering, registration, and visualization of tera-scale microscopy data. We evaluate the performance of our system using a leadership-class supercomputer, Shaheen II.


W. Usher, P. Klacansky, F. Federer, P. T. Bremer, A. Knoll, J. Yarch, A. Angelucci, V. Pascucci.
“A Virtual Reality Visualization Tool for Neuron Tracing,” In IEEE Transactions on Visualization and Computer Graphics, IEEE, 2017.
ISSN: 1077-2626
DOI: 10.1109/TVCG.2017.2744079
Tracing neurons in large-scale microscopy data is crucial to establishing a wiring diagram of the brain, which is needed to understand how neural circuits in the brain process information and generate behavior. Automatic techniques often fail for large and complex datasets, and connectomics researchers may spend weeks or months manually tracing neurons using 2D image stacks. We present a design study of a new virtual reality (VR) system, developed in collaboration with trained neuroanatomists, to trace neurons in microscope scans of the visual cortex of primates. We hypothesize that using consumer-grade VR technology to interact with neurons directly in 3D will help neuroscientists better resolve complex cases and enable them to trace neurons faster and with less physical and mental strain. We discuss both the design process and technical challenges in developing an interactive system to navigate and manipulate terabyte-sized image volumes in VR. Using a number of different datasets, we demonstrate that, compared to widely used commercial software, consumer-grade VR presents a promising alternative for scientists.
2016


C. Christensen, S. Liu, G. Scorzelli, J. Lee, P.-T. Bremer, V. Pascucci.
“Embedded Domain-Specific Language and Runtime System for Progressive Spatiotemporal Data Analysis and Visualization,” In Symposium on Large Data Analysis and Visualization, IEEE, 2016.
As our ability to generate large and complex datasets grows, accessing and processing these massive data collections is increasingly the primary bottleneck in scientific analysis. Challenges include retrieving, converting, resampling, and combining remote and often disparately located data ensembles with only limited support from existing tools. In particular, existing solutions rely predominantly on extensive data transfers or large-scale remote computing resources, both of which are inherently offline processes with long delays and substantial repercussions for any mistakes. Such workflows severely limit the flexible exploration and rapid evaluation of new hypotheses that are crucial to the scientific process and thereby impede scientific discovery. Here we present an embedded domain-specific language (EDSL) specifically designed for the interactive exploration of largescale, remote data. Our EDSL allows users to express a wide range of data analysis operations in a simple and abstract manner. The underlying runtime system transparently resolves issues such as remote data access and resampling while at the same time maintaining interactivity through progressive and interruptible computation. This system enables, for the first time, interactive remote exploration of massive datasets such as the 7km NASA GEOS-5 Nature Run simulation, which previously have been analyzed only offline or at reduced resolution.


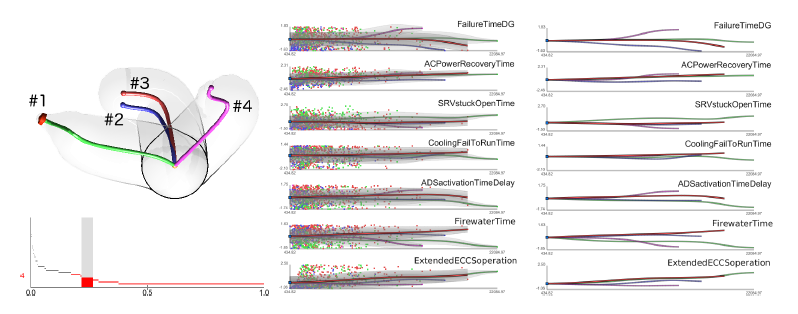
D. Maljovec, S. Liu, Bei Wang, V. Pascucci, P. T. Bremer, D. Mandelli, C. Smith..
“Analyzing Simulation-Based PRA Data Through Traditional and Topological Clustering: A BWR Station Blackout Case Study,” In Reliability Engineering & System Safety, Vol. 145, Elsevier, pp. 262--276. January, 2016.
DOI: 10.1016/j.ress.2015.07.001
Dynamic probabilistic risk assessment (DPRA) methodologies couple system simulator codes (e.g., RELAP, MELCOR) with simulation controller codes (e.g., RAVEN, ADAPT). Whereas system simulator codes model system dynamics deterministically, simulation controller codes introduce both deterministic (e.g., system control logic, operating procedures) and stochastic (e.g., component failures, parameter uncertainties) elements into the simulation. Typically, a DPRA is performed by sampling values of a set of parameters, and simulating the system behavior for that specific set of parameter values. For complex systems, a major challenge in using DPRA methodologies is to analyze the large number of scenarios generated, where clustering techniques are typically employed to better organize and interpret the data. In this paper, we focus on the analysis of two nuclear simulation datasets that are part of the risk-informed safety margin characterization (RISMC) boiling water reactor (BWR) station blackout (SBO) case study. We provide the domain experts a software tool that encodes traditional and topological clustering techniques within an interactive analysis and visualization environment, for understanding the structures of such high-dimensional nuclear simulation datasets. We demonstrate through our case study that both types of clustering techniques complement each other in bringing enhanced structural understanding of the data.


I. Rodero, M. Parashar, A.G. Landge, S. Kumar, V. Pascucci,, P.T. Bremer.
“Evaluation of in-situ analysis strategies at scale for power efficiency and scalability,” In Cluster, Cloud and Grid Computing (CCGrid), 2016 16th IEEE/ACM International Symposium on, IEEE, pp. 156--164. 2016.
The increasing gap between available compute power and I/O capabilities is resulting in simulation pipelines running on leadership computing facilities being reformulated. In particular, in-situ processing is complementing conventional post-process analysis; however, it can be performed by using the same compute resources as the simulation or using secondary dedicated resources.
In this paper, we focus on three different in-situ analysis strategies, which use the same compute resources as the ongoing simulation but different data movement strategies. We evaluate the costs incurred by these strategies in terms of run time, scalability and power/energy consumption. Furthermore, we extrapolate power behavior to peta-scale and investigate different design choices through projections. Experimental evaluation at full machine scale on Titan supports that using fewer cores per node for in-situ analysis is the optimum choice in terms of scalability. Hence, further research effort should be devoted towards developing in-situ analysis techniques following this strategy in future high-end systems.


W. Usher, I. Wald, A. Knoll, M. Papka, V. Pascucci.
“In Situ Exploration of Particle Simulations with CPU Ray Tracing,” In Supercomputing Frontiers and Innovations, Vol. 3, No. 4, 2016.
ISSN: 2313-8734
DOI: 10.14529/jsfi160401
We present a system for interactive in situ visualization of large particle simulations, suitable for general CPU-based HPC architectures. As simulations grow in scale, in situ methods are needed to alleviate IO bottlenecks and visualize data at full spatio-temporal resolution. We use a lightweight loosely-coupled layer serving distributed data from the simulation to a data-parallel renderer running in separate processes. Leveraging the OSPRay ray tracing framework for visualization and balanced P-k-d trees, we can render simulation data in real-time, as they arrive, with negligible memory overhead. This flexible solution allows users to perform exploratory in situ visualization on the same computational resources as the simulation code, on dedicated visualization clusters or remote workstations, via a standalone rendering client that can be connected or disconnected as needed. We evaluate this system on simulations with up to 227M particles in the LAMMPS and Uintah computational frameworks, and show that our approach provides many of the advantages of tightly-coupled systems, with the flexibility to render on a wide variety of remote and co-processing resources.
2015

J. Bennett, F. Vivodtzev, V. Pascucci (Eds.).
“Topological and Statistical Methods for Complex Data,” Subtitled “Tackling Large-Scale, High-Dimensional, and Multivariate Data Spaces,” Mathematics and Visualization, Springer Berlin Heidelberg, 2015.
ISBN: 978-3-662-44899-1
This book contains papers presented at the Workshop on the Analysis of Large-scale,
High-Dimensional, and Multi-Variate Data Using Topology and Statistics, held in Le Barp,
France, June 2013. It features the work of some of the most prominent and recognized
leaders in the field who examine challenges as well as detail solutions to the analysis of
extreme scale data.
The book presents new methods that leverage the mutual strengths of both topological
and statistical techniques to support the management, analysis, and visualization
of complex data. It covers both theory and application and provides readers with an
overview of important key concepts and the latest research trends.
Coverage in the book includes multi-variate and/or high-dimensional analysis techniques,
feature-based statistical methods, combinatorial algorithms, scalable statistics algorithms,
scalar and vector field topology, and multi-scale representations. In addition, the book
details algorithms that are broadly applicable and can be used by application scientists to
glean insight from a wide range of complex data sets.


J. Bennett, R. Clay, G. Baker, M. Gamell, D. Hollman, S. Knight, H. Kolla, G. Sjaardema, N. Slattengren, K. Teranishi, J. Wilke, M. Bettencourt, S. Bova, K. Franko, P. Lin, R. Grant, S. Hammond, S. Olivier, L. Kale, N. Jain, E. Mikida, A. Aiken, M. Bauer, W. Lee, E. Slaughter, S. Treichler, M. Berzins, T. Harman, A. Humphrey, J. Schmidt, D. Sunderland, P. McCormick, S. Gutierrez, M. Schulz, A. Bhatele, D. Boehme, P. Bremer, T. Gamblin.
“ASC ATDM level 2 milestone #5325: Asynchronous many-task runtime system analysis and assessment for next generation platforms,” Sandia National Laboratories, 2015.
This report provides in-depth information and analysis to help create a technical road map for developing nextgeneration programming models and runtime systems that support Advanced Simulation and Computing (ASC) workload requirements. The focus herein is on asynchronous many-task (AMT) model and runtime systems, which are of great interest in the context of "exascale" computing, as they hold the promise to address key issues associated with future extreme-scale computer architectures. This report includes a thorough qualitative and quantitative examination of three best-of-class AMT runtime systems—Charm++, Legion, and Uintah, all of which are in use as part of the ASC Predictive Science Academic Alliance Program II (PSAAP-II) Centers. The studies focus on each of the runtimes' programmability, performance, and mutability. Through the experiments and analysis presented, several overarching findings emerge. From a performance perspective, AMT runtimes show tremendous potential for addressing extremescale challenges. Empirical studies show an AMT runtime can mitigate performance heterogeneity inherent to the machine itself and that Message Passing Interface (MPI) and AMT runtimes perform comparably under balanced conditions. From a programmability and mutability perspective however, none of the runtimes in this study are currently ready for use in developing production-ready Sandia ASC applications. The report concludes by recommending a codesign path forward, wherein application, programming model, and runtime system developers work together to define requirements and solutions. Such a requirements-driven co-design approach benefits the high-performance computing (HPC) community as a whole, with widespread community engagement mitigating risk for both application developers and runtime system developers.


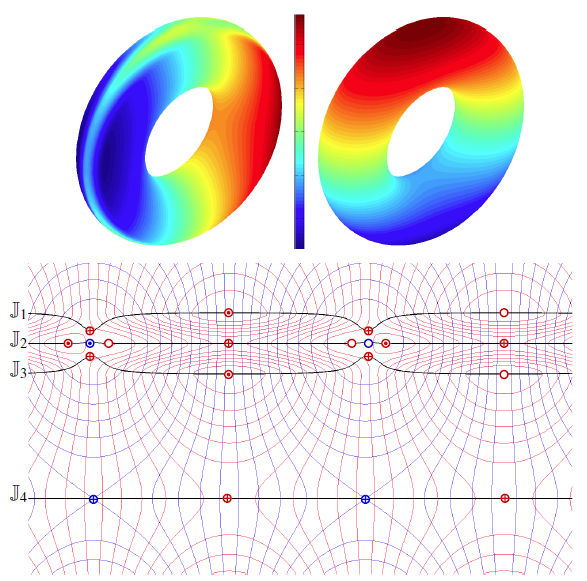
H. Bhatia, Bei Wang, G. Norgard, V. Pascucci, P. T. Bremer.
“Local, Smooth, and Consistent Jacobi Set Simplification,” In Computational Geometry, Vol. 48, No. 4, Elsevier, pp. 311-332. May, 2015.
DOI: 10.1016/j.comgeo.2014.10.009
The relation between two Morse functions defined on a smooth, compact, and orientable 2-manifold can be studied in terms of their Jacobi set. The Jacobi set contains points in the domain where the gradients of the two functions are aligned. Both the Jacobi set itself as well as the segmentation of the domain it induces, have shown to be useful in various applications. In practice, unfortunately, functions often contain noise and discretization artifacts, causing their Jacobi set to become unmanageably large and complex. Although there exist techniques to simplify Jacobi sets, they are unsuitable for most applications as they lack fine-grained control over the process, and heavily restrict the type of simplifications possible.
This paper introduces the theoretical foundations of a new simplification framework for Jacobi sets. We present a new interpretation of Jacobi set simplification based on the perspective of domain segmentation. Generalizing the cancellation of critical points from scalar functions to Jacobi sets, we focus on simplifications that can be realized by smooth approximations of the corresponding functions, and show how these cancellations imply simultaneous simplification of contiguous subsets of the Jacobi set. Using these extended cancellations as atomic operations, we introduce an algorithm to successively cancel subsets of the Jacobi set with minimal modifications to some userdefined metric. We show that for simply connected domains, our algorithm reduces a given Jacobi set to its minimal configuration, that is, one with no birth-death points (a birth-death point is a specific type of singularity within the Jacobi set where the level sets of the two functions and the Jacobi set have a common normal direction).


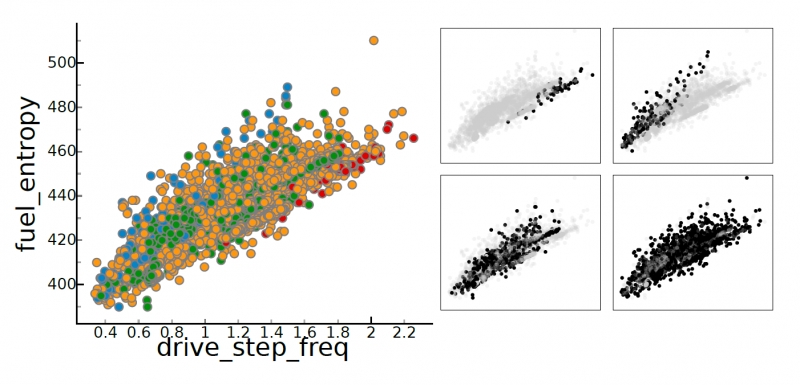
P. T. Bremer, D. Maljovec, A. Saha, Bei Wang, J. Gaffney, B. K. Spears, V. Pascucci.
“ND2AV: N-Dimensional Data Analysis and Visualization -- Analysis for the National Ignition Campaign,” In Computing and Visualization in Science, 2015.
One of the biggest challenges in high-energy physics is to analyze a complex mix of experimental and simulation data to gain new insights into the underlying physics. Currently, this analysis relies primarily on the intuition of trained experts often using nothing more sophisticated than default scatter plots. Many advanced analysis techniques are not easily accessible to scientists and not flexible enough to explore the potentially interesting hypotheses in an intuitive manner. Furthermore, results from individual techniques are often difficult to integrate, leading to a confusing patchwork of analysis snippets too cumbersome for data exploration. This paper presents a case study on how a combination of techniques from statistics, machine learning, topology, and visualization can have a significant impact in the field of inertial confinement fusion. We present the ND2AV: N-Dimensional Data Analysis and Visualization framework, a user-friendly tool aimed at exploiting the intuition and current work flow of the target users. The system integrates traditional analysis approaches such as dimension reduction and clustering with state-of-the-art techniques such as neighborhood graphs and topological analysis, and custom capabilities such as defining combined metrics on the fly. All components are linked into an interactive environment that enables an intuitive exploration of a wide variety of hypotheses while relating the results to concepts familiar to the users, such as scatter plots. ND2AV uses a modular design providing easy extensibility and customization for different applications. ND2AV is being actively used in the National Ignition Campaign and has already led to a number of unexpected discoveries.